分子計算では、安定配座間の遷移状態も求めることが出来ます。
考え方は構造最適化とよく似ていて、構造最適化では配座-立体エネルギーダイヤグラムの曲線を下っていくのに対して、遷移状態計算では、極大値となる配座を求めます。ただし、単純な極大値ではありません。
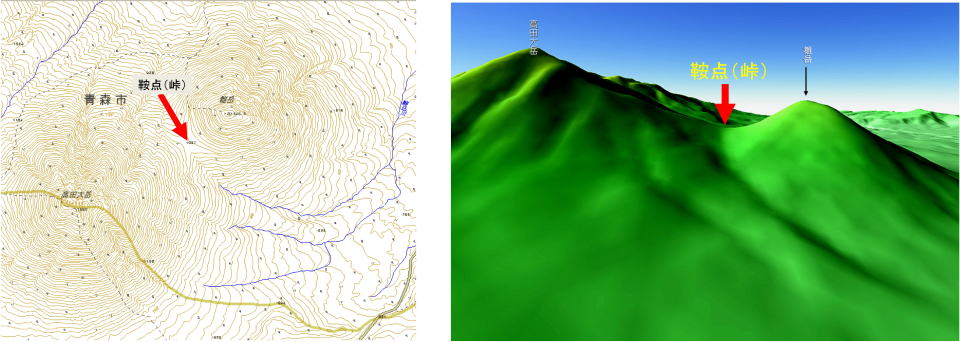
遷移状態とは一番高くて低いところで、数学用語では鞍点（saddle point）と言います。下の図ではいわゆる「峠」がそれにあたります。人が下の地図で、南東（右下）から北西（左上に）進むとします。体力が有り余っている人や、山登りが趣味である人を除いて、できるだけ労力の小さくなる峠を越えていきます。（山を迂回するという話はここではなしです。）　峠はその人が歩く道筋の中では最も標高が高くなりますが、他のルートに比べれば最も低い標高を通ることになります。別の見方をしましょう。我々が、山むこうの町にドライブするとき、車はどんどん高度を上がって行きます。そして最高地点を通り過ぎ、車は高度がさがり目的の町に到着します。遷移状態とはこのドライブの最高地点と考えることができます。通常、山越えの道の最高地点は、観光道路を別にすれば峠と呼ばれる最高地点の中で最も低いところです。道路としては最高地点ですが、峠で車をおりて、周りを見渡すと周りにはより高い山がそびえています。遷移状態はまさに「峠」のような地点です。
　

N個の原子からなる分子の遷移状態の鞍点は（３N-６）次元の平面での鞍点を求めることになりますので、数学的に解を得るのは難しいとされています。
たとえば、ブタンのC2-C3位に関するメチル基同士がsyn配置となるeclipse配座を求めようとしましょう。言うまでもなくこの配座は遷移状態です。しかし、メチル基同士の二面角が120度となった配座も遷移状態ですし、C1-C2結合のeclipse配座も遷移状態です。さらに、結合が切れていく開裂反応の遷移状態まで存在します。「高くて低いところを求めろ」といっても、もっと詳しい指示を与えなければコンピュータは迷ってしまいます。実際に遷移状態計算を試みると、エネルギーは収束するどころか発散してしまいエラーとして停止してしまうことをよく経験します。遷移状態計算では安定配座を初期配座とすることは出来ません。入力ファイルによっては、収束せずに永久にiterationを繰り返すときもあります。運よくエネルギーが収束しても、目的出ない遷移状態が得られることは珍しくありません。
正しい答えを求めるには、初期配座を求める遷移状態にできるだけ近い形にする必要があります。。したがって、遷移状態計算では、遷移状態に出来るだけ近い構造を初期配座として用いる必要があり、有機化学の知識・センスを必要とします。

反応の遷移状態も全く同じ手法で行うことが出来ます。計算結果を状態-生成熱ダイヤグラムとして考えるだけの違いです。遷移状態の計算でも初期配座は重要です。初期配座Aを用いて計算した場合、状態Pへの遷移状態Xの配座を求めることが出来ます。一方初期配座をBとした場合は、それとは異なった状態Qへの遷移状態Yを計算結果として与えます。